Physics Modeling and Verification

Neutron Transport and Cross Sections

GUARDYAN uses the cross section data table ENDF/B-VII.1 in ACE (A Compact ENDF) format. Interaction sampling follows similar techniques as in MCNP and OpenMC (​OpenMC). Albeit not optimal for GPU applications, we have chosen the already paved way in order to create an easily verifiable code. Major efficiency gain is expected from transforming interaction sampling towards eliminating rejection steps even in exchange for particle weight change: the latter being disadvantageous for the statistical variance the former minimizing thread divergence.

Free path sampling follows the Woodcock (delta-tracking) scheme with energy dependent majorant sampling cross section. The selection of isotope and interaction type happens in the analog way except for choosing between scattering and fission events.

We consider reactions with the following MT numbers: 2, 5, 11, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 28, 29, 30, 32, 33, 34, 35, 36, 37, 38, 41, 44, 45, 51-90, 101. After choosing the reaction, the determination of the new energy and angle of the neutron depends on the given ACE law (ACE Laws 3, 4, 7, 9, 11, 44, 61 or 66 ). S($\alpha$, $\beta$) treatment and handling unresolved resonances are also included in the physics modeling.

Verification

Verification Methodology

Often a verification of a newly implemented reactor physics code is done in an integral sense, on a near critical assembly with complicated geometry and the estimation of integral parameters like the k_eff is compared to a well established code calculation result. As GUARDYAN is meant primarily to simulate time evolution of power level and flux we have decided to compare time and energy spectra separately for a broad selection of isotopes. A small subcritical model was also created for validating geometry features and isotope mixture handling.

The verification basic model was a sphere containing a single isotope with density belonging to the natural isotope abundance. Neutrons were started at time zero. In separate calculations 5 starting energies were selected: 10^-8, 10^-6, 10^-3, 1, 18 MeV thereby the interaction types for the full relevant energy range (from thermal up to the energy limit of commonly available cross section data). For each isotope the radius of the sphere was set to three times the free path length at the neutron starting energy. First GUARDYAN was executed and the particles registered at the outer bounding surface of the sphere. Next, using smallest and largest values of energy and time of the GUARDYAN samples a tally bin structure is set up with 24 logarithmic energy bins and 9 equally spaced time bins. MCNP6 input was generated and executed with these tally settings.

The list of isotopes includes every isotope present in ENDF/B-VII.1, except for the metastable ones.

The subcritical model was a 30 cm radius water sphere with 61 UO₂ cylindrical fuel rods of 40 cm length, 1 cm radius spaced 1 cm apart from each other see Fig. 1.. Uranium was 4.7% enriched and fuel rod density was taken as 10.5g/cm³.

Figure 1.: Geometry of the subcritical verification model

Similarly, a time-energy spectrum is registered in this case as well.

Verification Results - simple spherical geometry

For each isotope a figure has been created for visual inspection see Fig. 2. Separate figures are energy spectra of the number of particles crossing the sphere outer surface divided by the starting particle number, each figure belongs to a separate time interval.

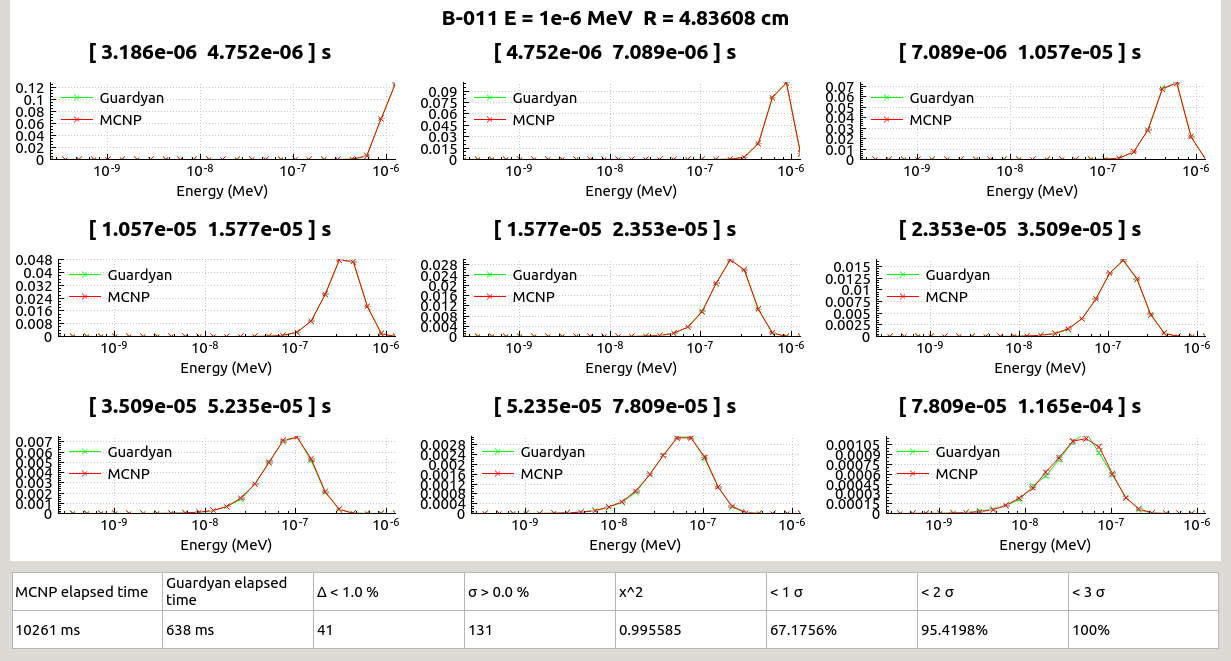
Figure 2.: Example of Time-Energy Spectra comparison graphs for ¹¹Be, 10^-6 MeV

As a result a total of some 445 000 data points were compared at the final stage. A reduced $\chi$² -like statistics was calculated as:

$\chi ^{{2}=\frac{1}{N}\sum_{i=1}}{N}\frac{(y_{MCNP,i}-y_{GUARDYAN,i})^{{2}}{\sigma_{MCNP,i}}{2}-\sigma_{GUARDYAN,i}^{2}}$

where N is the number of i data points for a single isotope a single starting energy (i.e. N= 9x 24 = 216 ), $\sigma$ stands for the standard deviation of the Monte Carlo estimates and y is the tally results. It means that squared difference is compared against the sum of squared standard deviations, thus $\chi$² should be below 1 is if the results fall within 1 standard deviation, in most cases it should be below 2 and results above 3 should be rare.

With each $\chi$² calculated, we obtain N= 412 x 5 energies . These results are summarized in Fig.3. in a histogram.

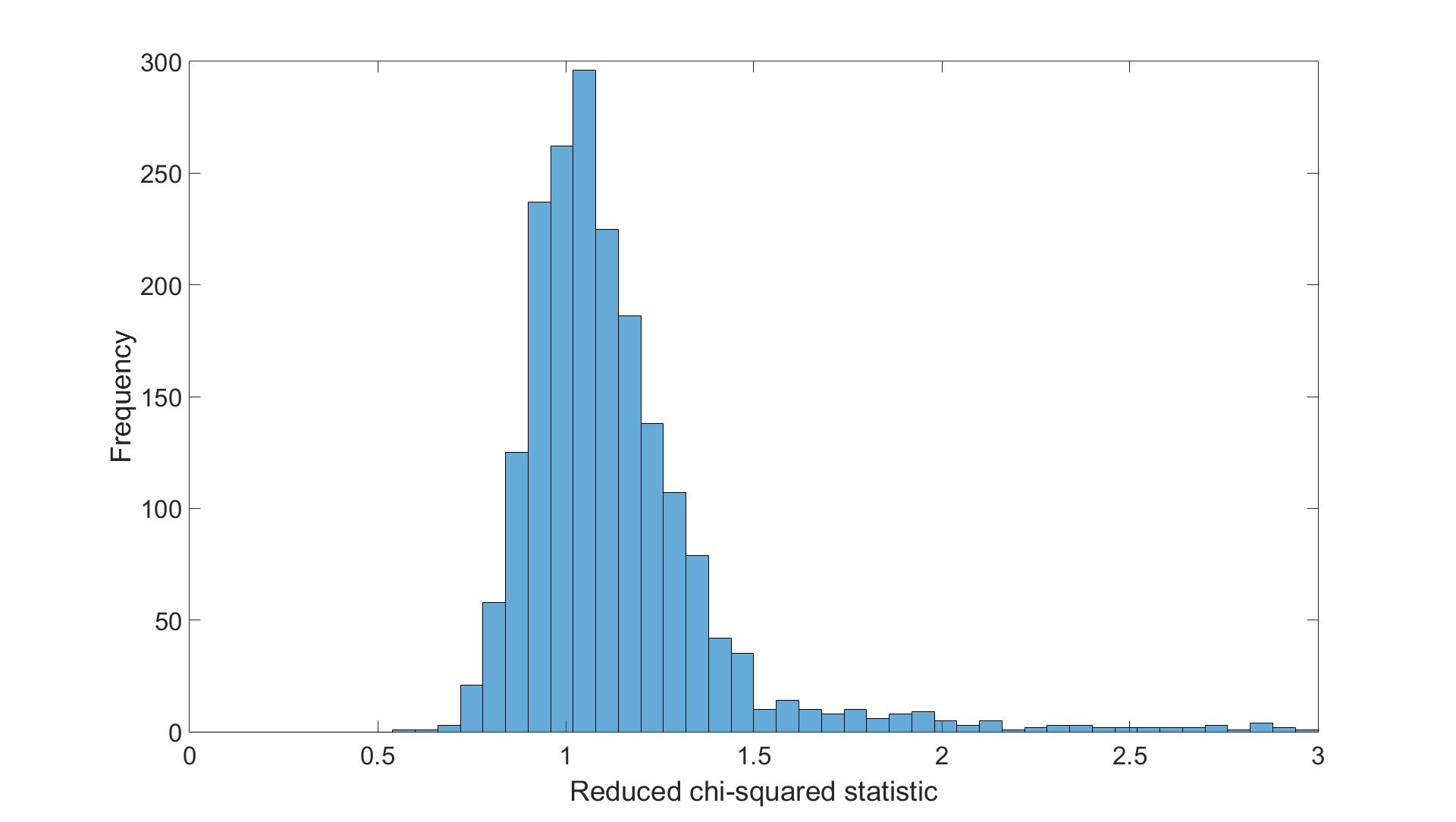
Figure 3.: Reduced $\chi$² histogram

As Fig. 3 shows GUARDYAN and MCNP results agree very well within statistics having the majority of the cases with match within 1.5$\sigma$.

For lower energies, in vast majority of the isotopes the dominant interaction is elastic scattering. For fissionable materials ACE laws 3, 4, 7, 9, 11, 44, 61 and 66 occur even at low energies, for higher energies many isotopes undergo such interactions, still elastic scattering being the dominant interaction in case of the basic model. To ensure that promising $\chi$² values are not only caused by a properly implemented elastic scattering algorithm, we have registered the number of samplings of certain ACE laws. To assess the impact of a certain ACE law on the $\chi$² value we have calculated the (Pearson) correlation coefficient between x_i and y_i data points with $\overline{x}$ and $\overline{y}$ averages respectively:

$corr=\frac{\sum_{N}^{{i=1}\left ( x_{i}-\overline{x} \right )\left ( y_{i}-\overline{y} \right )}{\sqrt{\sum_{N}}{i=1}\left ( x_{i}-\overline{x} \right )^{{2}}\sqrt{\sum_{N}}{i=1}\left ( y_{i}-\overline{y} \right )^{2}}}$

Table I. shows the correlation of the number of a certain ACE law sampling with the $\chi$² values for different neutron starting energies. Near zero correlation coefficients indicate no correlation, near 1 or -1 strong linear correlation.

Elastic scattering appears always with near zero coefficients with consistently negative sign. At 10-8 MeV and 18MeV the correlation is greater but still negative; we may interpret this as elastic scattering contributing to better match of results. ACE Law 3 (inelastic level scattering), ACE Law 4 (continuous tabular distribution) and ACE Law 61 (correlated energy and angle distribution) show a clearly nonzero and often positive correlation indicating that the GPU implementation differ from MCNP. All three of these sampling processes happen with high energy neutrons, for low starting neutron energies the interactions happen after fission has occurred. Number of sampled interactions with these laws shows that without fissile material present, none of these sampling processes are called.

10-8 MeV		10-6 MeV	10-3 MeV	1MeV	18Mev
Elastic scattering	-0.21372	-0.01053	-0.05259	-0.07189	-0.26171
ACE Law 3	0.4743	0.43175	0.41582	-0.05454	-0.15467
ACE Law 4	0.30463	0.32031	0.67385	0.45868	0.17577
ACE Law 7	-0.00399	-0.00405	0.01045	-0.00808	-0.00166
ACE Law 9	-0.00872	-0.00649	0.01524	-0.00716	0.03139
ACE Law 11	-0.01198	0.00382	0.05435	0.00464	0.00769
ACE law 44	0.00206	-0.00254	0.04434	0.14184	-0.03327
law61	0.31364	0.21316	0.50553	-0.00556	-0.09562
law66	--	--	--	--	-0.00607

Table I. Correlation of $\chi$² values with number of sampling of a certain ACE law

ACE Law 3 and 61 for higher starting neutron energies show almost zero correlation coefficient, i.e. at energies where the ratio of sampling number to elastic scattering is the highest, yielding the conclusion that the law sampling is less to suspect. For fissile materials the simulation chain lengths vary with number of collisions in a chain following geometrical distribution yielding a less robust estimation. ACE Law 4 shows the same behavior but higher energies still show higher correlation coefficients while this sampling process is very often called for most of the isotopes. Further research will target the solution of this issue.

Verification Results - Simple subcritical assembly

Results for the subcritical model is shown in Fig. 4.

Neutrons were started again in the middle of the geometry, with 10MeV starting energy. In the first three time intervals the neutrons thermalize and from the fourth time step on fission neutrons start to appear, and for the last time step the fission neutrons dominate the spectrum again. For this process neutrons had to transverse geometry, select interaction, slow down by scattering reactions, captured by absorption and finally escape or induce fission. As Fig. 6 shows every important reaction for a reactor neutronics is sampled and the previously shown isotope-by-isotope validation process also matches MCNP results for a –though very simplified, but still a - reactor application

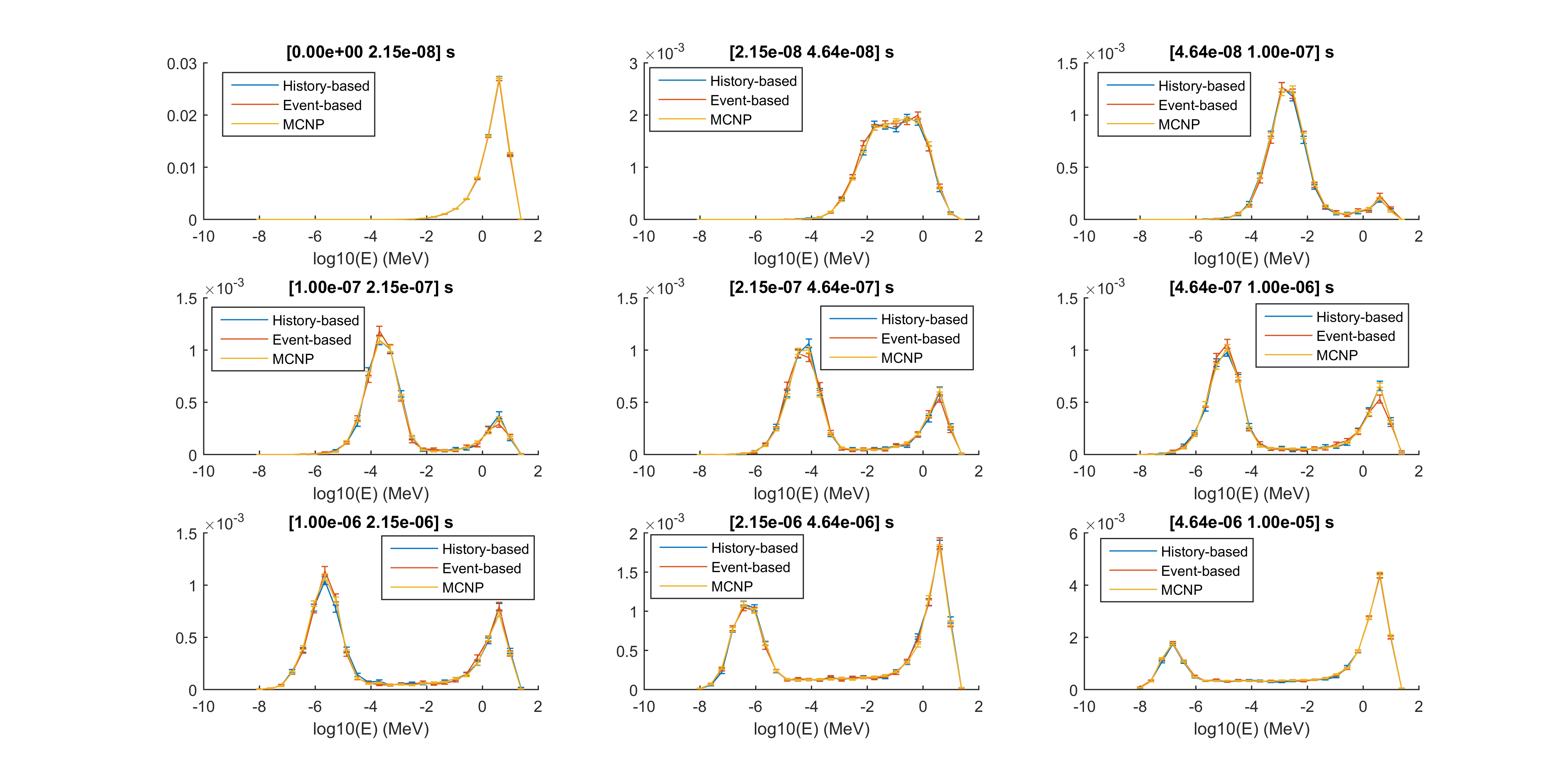
Figure 4.: Verification results for a subcritical assembly

next: Variance Reduction

---